Diferansiyel Geometri Serisi 8. Bölüm

Yüzeyler Teorisi: Pürüzsüzlük, Tuzaklar ve Gerçek Dünya

Selamlar! Diferansiyel geometri serimizin 8. bölümüne hoş geldiniz. Geçen bölümlerde tek boyutlu eğrilerin peşinden koştuk, Frenet çatısı ile virajları aldık. Şimdi ise boyut atlıyoruz. Artık üzerinde yürüyebileceğimiz, harita çizebileceğimiz, hatta üzerine kahve dökebileceğimiz yapılarla, yani Yüzeyler ile ilgileneceğiz.

Ama uyarayım, yüzeyler eğrilerden daha kaprislidir. Her $f(x,y)$ grafiği bize dost olmaz. Bu bölümde hem dostlarımızı tanıyacağız hem de "yüzey gibi görünen ama aslında baş belası olan" yapıları ifşa edeceğiz.

Yüzey Nedir? (Biraz Daha Formalite)

Bir küme düşünün uzayda süzülen. Biz buna ne zaman "düzgün yüzey" deriz? Matematikçiler olarak "göze hoş geliyor" diyemeyiz. Elimizde daha sağlam bir tanım olmalı.

Tanım (Düzenli Yüzey)

$S \subset \mathbb{E}^3$ bir alt küme olsun. Eğer her $p \in S$ noktası için, $p$ 'yi içeren bir $V \subset S$ komşuluğu ve $U \subset \mathbb{R}^2$ açık kümesinden $V$ 'ye giden bir $\mathbf{x}: U \rightarrow V$ dönüşümü varsa ve bu dönüşüm şu üç şartı sağlıyorsa, $S$ 'ye düzenli yüzey denir:

Diferansiyellenebilirlik: $\mathbf{x}$ fonksiyonunun her mertebeden kısmi türevleri var ve sürekli. (Yani yüzeyde ani kırılmalar, keskin köşeler yok, "kaymak" gibi.)
Homeomorfizm: $\mathbf{x}$ birebir, örten ve tersi de sürekli olmalı. (Yani yüzey kendi üzerine katlanmamalı, düğümlenmemeli. Kağıdı buruşturup top yapabilirsiniz ama yırtıp içinden geçiremezsiniz.)
Düzenlilik (Regularity) Şartı: Her $(u,v) \in U$ için diferansiyel dönüşüm birebir olmalı. Pratikte bu şu demektir:

\mathbf{x}_u \wedge \mathbf{x}_v \neq \mathbf{0}

Bu üçüncü madde hayati önem taşır. Çünkü $\mathbf{x}_u$ ve $\mathbf{x}_v$ vektörleri, yüzeyin o noktadaki "teğet düzlemini" geren vektörlerdir. Eğer bunların vektörel çarpımı sıfırsa, ya vektörlerden biri sıfırdır ya da birbirlerine paraleldirler. Bu durumda orada bir düzlem oluşmaz, yüzey "büzüşür" veya "sivrilir".

Karşıt Örnekler: İşler Nerede Sarpa Sarar?

Her gördüğümüz şekil yüzey değildir. Tanımdaki şartların neden gerekli olduğunu anlamak için "bozuk" örneklere, yani karşıt örneklere bakalım.

Örnek A: Koni (Sivri Uç Problemi)

Bildiğimiz dondurma külahını düşünün. Matematiksel olarak $z = \sqrt{x^2 + y^2}$ denklemiyle verilir. Parametrizasyonu şöyle yapabiliriz:

\mathbf{x}(u, v) = (u \cos v, u \sin v, u)

Burada $u$ yarıçap ( $u \ge 0$ ), $v$ ise açıdır.

Türevlere bakalım:

$\mathbf{x}_u = (\cos v, \sin v, 1)$
$\mathbf{x}_v = (-u \sin v, u \cos v, 0)$

Şimdi vektörel çarpımı hesaplayalım:

\mathbf{x}_u \wedge \mathbf{x}_v = (-u \cos v, -u \sin v, u)

Bu vektörün uzunluğu (normu):

\sqrt{u^2 \cos^2 v + u^2 \sin^2 v + u^2} = \sqrt{2u^2} = u\sqrt{2}

Dikkat! Eğer $u = 0$ ise (yani koninin tam tepe noktasındaysak), norm sıfır olur!

\mathbf{x}_u \wedge \mathbf{x}_v = \mathbf{0}

Bu demektir ki, koninin tepe noktasında bir teğet düzlem tanımlayamayız. O nokta "sivri"dir. Dolayısıyla koni, tepe noktası hariç düzenli bir yüzeydir, ama tepe noktası işin içine girerse düzenli yüzey değildir. Diferansiyel geometri o sivri ucu sevmez.

Örnek B: Kendi Kendini Kesen Yüzeyler

Eğer dönüşümümüz birebir değilse (Tanım madde 2 ihlali), yüzey kendi içinden geçer. Mesela "Klein Şişesi" 3 boyutlu uzayda kendini kesmeden çizilemez (4 boyuta ihtiyacı vardır). 3 boyutta çizmeye kalkarsanız bir yerlerde kendini kesmek zorunda kalır. Kendini kestiği noktalarda teğet düzlem "iki tane" olur ki bu da bizim fonksiyon olma mantığımıza aykırıdır.

Uygulamalar: Bu Matematik Nerede Kullanılıyor?

"Hocam iyi güzel de, koninin ucunun sivri olduğunu zaten gözümle görüyorum, türeve ne gerek var?" diyebilirsiniz. Haklısınız ama bu teorinin uygulama alanları çok geniştir.

Uygulama 1: Bilgisayar Grafikleri ve Oyun Motorları

Oynadığınız o yüksek çözünürlüklü oyunlardaki karakterlerin yüzleri, arabaların kaportaları aslında birer "yüzey yaması"dır (Bezier yüzeyleri veya NURBS). Oyun motoru, ışığın o yüzeyden nasıl yansıyacağını hesaplamak için Normal Vektöre ( $N$ ) ihtiyaç duyar.

N = \frac{\mathbf{x}_u \wedge \mathbf{x}_v}{||\mathbf{x}_u \wedge \mathbf{x}_v||}

Eğer sizin modelinizde koni gibi "sivri" bir nokta varsa ve matematiksel olarak orayı düzgün tanımlamadıysanız, oyun motoru orada normal vektörü hesaplayamaz (0'a bölme hatası) ve orada ışıklandırma "patlar" (siyah lekeler veya garip parlamalar görürsünüz).

Uygulama 2: Kartografya (Haritacılık)

Dünya yuvarlaktır (Küreye yakın), kağıt ise düzdür. Bir küre yüzeyini ( $\mathbb{E}^3$ 'te bir yüzey), düzleme ( $\mathbb{R}^2$ 'ye) aktarma işlemine biz parametrizasyonun tersi diyoruz.

Diferansiyel geometri bize şunu söyler: Kürenin "Eğriliği" (Gauss Eğriliği, ileride göreceğiz) pozitiftir, düzlemin eğriliği sıfırdır. Bu yüzden, küreyi düzleme, mesafeleri ve açıları bozmadan aktarmak imkansızdır. Yani haritalarınızın hepsi yalan söylüyor! Ya Grönland'ı çok büyük gösteriyorlar (Mercator projeksiyonu) ya da şekilleri yamultuyorlar. Bu matematiksel bir zorunluluktur.

Python ile "Bozuk" ve "Düzgün" Yüzey Karşılaştırması

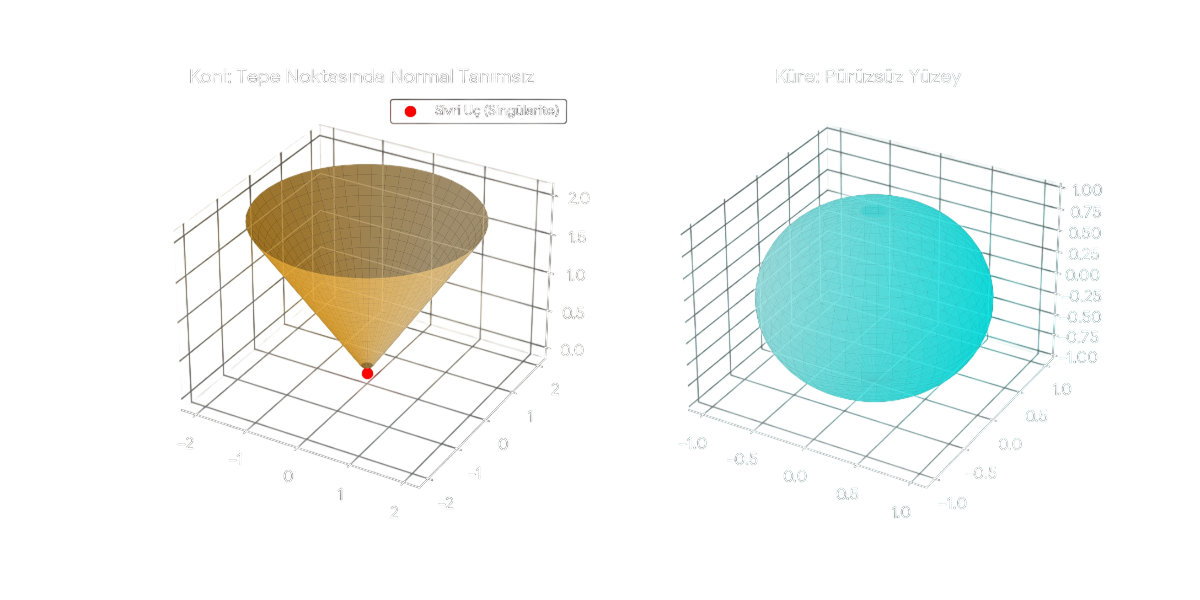
Teorik olarak bahsettiğimiz bu "regülerlik" kavramını görselleştirmek, meseleyi anlamak açısından kritiktir. Bir küreyi ve bir koniyi ele alalım. Küre, her noktasında pürüzsüzdür ve her noktasında tek bir normal vektörü (yüzeye dik çıkan ok) tanımlanabilir.

Ancak koninin tepe noktasına $(0,0,0)$ geldiğimizde işler karışır. Bu noktada yüzey "sivrilir" ve matematiksel olarak $\mathbf{x}_u \times \mathbf{x}_v = 0$ durumu oluşur. Yani koninin tepesinde teğet düzlemi tanımlanamaz; dolayısıyla burası bir singülarite (tekillik) noktasıdır.

Aşağıdaki Python kodu, bu iki yüzey arasındaki temel farkı görselleştirmektedir:

import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure(figsize=(12, 6))

# --- KONI: Reguler olmayan nokta barındırır ---
u = np.linspace(0, 2*np.pi, 50)
v = np.linspace(0, 2, 20)
U, V = np.meshgrid(u, v)
X = V * np.cos(U); Y = V * np.sin(U); Z = V

ax1 = fig.add_subplot(121, projection='3d')
ax1.plot_surface(X, Y, Z, color='orange', alpha=0.6)
ax1.set_title("Koni: Tepe Noktası Problemlidir")
ax1.set_box_aspect((1, 1, 1)) # Ölcek duzeltme

# --- KURE: Her noktada regulerdir ---
v_s = np.linspace(0, np.pi, 30)
U_s, V_s = np.meshgrid(u, v_s)
X_s = np.sin(V_s) * np.cos(U_s); Y_s = np.sin(V_s) * np.sin(U_s); Z_s = np.cos(V_s)

ax2 = fig.add_subplot(122, projection='3d')
ax2.plot_surface(X_s, Y_s, Z_s, color='cyan', alpha=0.6)
ax2.set_title("Kure: Puruzsuz ve Reguler")
ax2.set_box_aspect((1, 1, 1))

plt.show()

Şekil 1– Koni ve Küre karşılaştırması. Koni örneğinde tepe noktasında yüzeyin normalinin tanımlanamaz oluşu, onu regüler bir yama olmaktan çıkarır.

Sonuç

Görüleceği üzere, diferansiyel geometri yapmak istiyorsak yüzeyimizin "pürüzsüz" olması (en azından çalıştığımız bölgede) şarttır. Gelecek bölümde, bu pürüzsüz yüzeyler üzerinde nasıl ölçüm yapacağımızı (Birinci Temel Form) öğreneceğiz.