Diferansiyel Geometri Serisi 7. Bölüm

Diferansiyel Geometri Serisi 7. Bölüm: Koklayarak Eğri Bulma Sanatı

Giriş: Menüde ne var?

Herkese merhaba, geçtiğimiz yazıda Frenet çatısının en temel iki kavramı olan eğrilik ve burulma üzerine kalem sallamıştık, bu yazıda ise eğrilik ve burulma üzerinden bir eğrinin yapısını anlamaya çalışacağız.

Eğri Büğrü bi' eğri!

Bu bölüm aslında bir bölümden ziyade bir örnek gösterimi olacak. Eğriliği $\kappa$ ve $\tau$ arasında $\frac{\kappa}{\tau}=sbt\neq 0, \forall s$ ilişkisi bulunan bir $\alpha$ eğrisi düşünelim, eğrilerin temel teoremine göre böyle bir eğri vardır, biz bu eğriyi açık biçimde sınıflandırabilir miyiz? Malum sabitimiz bir $\theta$ açısı için $\tan\theta$'ya eşit olduğunu kabul edelim. Böyle bir kabul yapmamızdaki motivasyon tanjant fonksiyonunun örten olmasından geliyor.

O halde $\kappa\cos\theta-\tau\sin\theta=0$ olacaktır. O halde $\alpha$ eğrisinin normal vektörü $\mathbf{N}$ için $(\kappa\cos\theta-\tau\sin\theta)\mathbf{N}=0$ olur. Neden normal vektörü işin içine soktuk? Çünkü eğrilik ve burulmanın normal vektör ile çarpıldığı durumlar bize sırayla tanjant ve binormal vektörün türevlerini verir de ondan. Buradan bir biçimde ilerleyebileceğiz. O halde az evvel yazdığımız denklem:

$$\cos\theta\ \mathbf{T}'+\sin\theta \ \mathbf{B}'= 0$$

halinde yazılabilir ve buradan

$$u:=\cos\theta \ \mathbf{T}+\sin\theta\ \mathbf{B}$$

birim vektörünü tanımlamamıza olanak sağlanır. Bu vektör $\mathbf{T}$ ile arasında $\theta$ kadar sabit bir açıya sahiptir. Teğeti bir doğrultu ile sabit açıya sahip eğriye helis dendiğini biliyoruz (bilmiyorsak da şimdi öğrendik), dolayısıyla eğriliği ve burulması arasındaki oran sıfırdan farklı bir sabit olan eğriler bir helis belirtir diyebiliriz. Aşağıda bu yaptıklarımızın Pythonca'sı mevcuttur.

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def helix(theta, t_range=np.linspace(0, 10, 500)):  
    kappa = np.cos(theta)
    tau = np.sin(theta)  # Burulma
    x = np.cos(kappa * t_range)
    y = np.sin(kappa * t_range)
    z = tau * t_range
    return x, y, z

thetas = np.linspace(0, np.pi/2, 5)
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

for theta in thetas:
    x, y, z = helix(theta)
    ax.plot(x, y, z, label=f"theta={np.degrees(theta):.0f}")

ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
ax.legend()
ax.set_title("Farkli Theta Acilari icin Helis Egrileri")
plt.show()

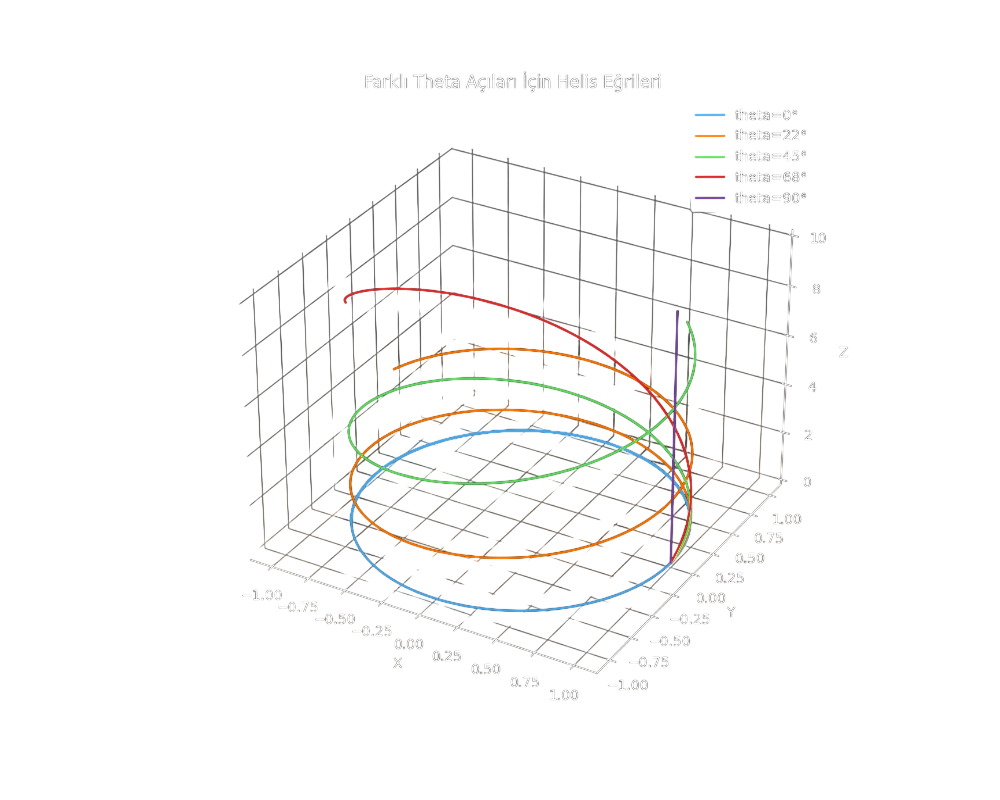
Burada açının $0$ ve dik olduğu durumları kendinizin yorumlamasını isteyeceğim. Bu esnada biz devam edelim. Görüyorsunuz ki sadece eğrilik ve burulma arası bir ilişkiden bir eğrinin ne olduğunu bulabiliyoruz. Bir sonrakiğ örneğimiz ile devam edelim.

Örnek

Tekrarda üç boyutlu Öklid uzayımız(aksi belirtilene kadar bu uzayda takılacağımızı söylemiş miydim? Söylemediysem şimdi söylemiş olayım.) içerisinde eğriliği sabit düzlemsel bir eğri düşünelim, yani $\tau=0$ olacaktır. Buradan bu eğrinin bir helis olmadığını hemen söyleyebiliriz, peki bu eğri nedir? Hemen Frenet çatısını yazalım.

$$\begin{bmatrix}\textbf{T}'\\\textbf{N}'\\\textbf{B}'\end{bmatrix} = \begin{bmatrix}0 & \kappa & 0 \\-\kappa& 0& 0 \\ 0& 0& 0\end{bmatrix} \begin{bmatrix}\textbf{T}\\\textbf{N}\\\textbf{B}\end{bmatrix}$$

burada $\kappa$'nın sabit olduğunu da göz önünde bulundurursak $\textbf{B}=\textbf{B}_0$, yani sabit bir vektör, $\textbf{T}''=-\kappa^2\textbf{T}$ çıkar ki burada yolumuz ikiye ayrılır. Eğer $\kappa=0$ ise $\alpha$ eğrimiz bir doğru çıkacaktır, fakat $\kappa\neq 0$ ise teğet vektörünün sinüsler ve kosinüslerin uğrak mekanı olduğunu anlayabiliriz. Buradan bu eğrinin çember olduğu fikri ortaya atılabilir. Lakin bu aslında bir iddiadan fazlasıdır, bu denklem çözülüp normal vektör için olan denklemde de yerine konursa görülür ki eğrimiz aslında bir çemberdir, hatta yarıçapı da $\frac{1}{\kappa}$'dır. Önceki bölümlerde hatırlayacağınız üzere teğet çemberden bahsetmiştim, şimdi bir 'wow' olmanız gerekiyor, bilginize...

Kıssadan hisse, bir eğrinin teğeti ve burulmasından yola çıkarak eğriyi direkt bulabilirsiniz. Bunun için biraz diferansiyel denklem çözmeniz gerekebilir ama günün sonunda bulacaksınızdır. Şimdi biz eğrilerle ilgili son sözleri söylemeye başlayalım, bir eğrinin 'indicatrix' leri ve 'evolute'u üzerine konuşalım.

Tanım (Teğet göstergesi / indicatrix)

$\alpha:I\rightarrow\mathbb{R}^3$ yay uzunluğu parametresine sahip bir düzgün eğri ve $\textbf{T}_\alpha(s)$ bu eğrinin $s$ noktasındaki teğeti olmak üzere, $\beta:I\rightarrow\mathbb{R}^3$, $\beta(s):=\textbf{T}_\alpha(s)$ olarak tanımlanan eğri bu eğrinin teğet göstergesi(indicatrix) denir.

Tanım (Normal göstergesi / indicatrix)

$\alpha:I\rightarrow\mathbb{R}^3$ yay uzunluğu parametresine sahip bir düzgün eğri ve $\textbf{N}_\alpha(s)$ bu eğrinin $s$ noktasındaki normali olmak üzere, $\gamma:I\rightarrow\mathbb{R}^3$, $\gamma(s):=\textbf{N}_\alpha(s)$ olarak tanımlanan eğri bu eğrinin normal göstergesi(indicatrix) denir.

Tanım (Binormal göstergesi / indicatrix)

$\alpha:I\rightarrow\mathbb{R}^3$ yay uzunluğu parametresine sahip bir düzgün eğri ve $\textbf{B}_\alpha(s)$ bu eğrinin $s$ noktasındaki binormali olmak üzere, $\mu:I\rightarrow\mathbb{R}^3$, $\mu(s):=\textbf{B}_\alpha(s)$ olarak tanımlanan eğri bu eğrinin binormal göstergesi(indicatrix) denir.

Birçok kaynakta yukarıda tanımlanan göstergelere 'spherical indicatrix' dendiğini görebilirsiniz, bunun sebebi aslında göstergelerin hepsinin birim vektör olması ve günün sonunda bir küre üstünde yaşaması gerektiğindendir. Şimdi bu göstergeler arasında en sık karşımıza çıkan teğet göstergesinin Frenet çatısını veren teoremimize değinelim.

Teorem

$\alpha:I\rightarrow\mathbb{R}^3$ yay uzunluğu parametresine sahip bir düzgün eğri ve $\beta:I\rightarrow\mathbb{R}^3$ eğrisi $\alpha$'nın teğet göstergesi olmak üzere, $\beta$'nın teğet, normal, binormal vektörleri ve eğriliği ile burulması aşağıdaki gibidir.

$$\begin{aligned} \textbf{T}_\beta&=\textbf{N}_\alpha \\ \textbf{N}_\beta&=-\frac{\kappa_\alpha\textbf{T}_\alpha+\tau_\alpha\textbf{N}_\alpha}{\sqrt{\kappa_\alpha^2+\tau_\alpha^2}}\\ \textbf{B}_\beta&=\frac{\kappa_\alpha\textbf{B}_\alpha-\tau_\alpha\textbf{T}_\alpha}{\sqrt{\kappa_\alpha^2+\tau_\alpha^2}}\\ \kappa_\beta &=\frac{\kappa_\alpha^2+\tau_\alpha^2}{\kappa_\alpha^2}\\ \tau_\beta &=\frac{\kappa_\alpha\tau_\alpha'-\kappa_\alpha'\tau_\alpha}{\kappa_\alpha(\kappa_\alpha^2+\tau_\alpha^2)} \end{aligned}$$

Lemma

Düzlemsel bir eğrinin teğet göstergesi birim çemberdir.

Örnek

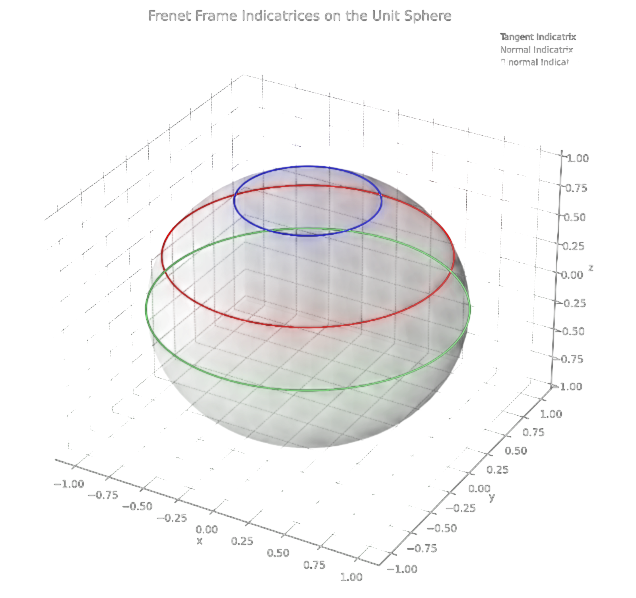
$\alpha(t)=(\cos t,\sin t, t)$ eğrisi bir helis belirtir(kanıtlayın). Bu eğrinin teğet, normal ve binormal göstergeleri aşağıda verilmiştir.

Bir Eğri'nin Evolute'u

Yine tam Türkçeleştiremediğim bir kavram. Her zamnki gibi elimize dünya güzeli bir $\alpha$ eğrisi alalım. Bu eğrinin bir $s$ için eğrilik yarıçapının $\frac{1}{\kappa(s)}$ olduğunu biliyoruz. Ortada bir yarıçap varsa bir çember de vardır elbette, şimdiki amacımız o çemberin merkezini lokal koordinatlarda bulmak. Bunun için Frenet çatısını göz önünde bulunduralım, biz normal vektörü $\textbf{T}'$ vektörünün yönünü belirten birim vektör olarak tanımalmıştık, ayrıca teğete dik olduğunu biliyoruz. Ayrıca eğriliğin işaretine göre $\textbf{T}'$ vektörünün yönünün değiştiğini de biliyoruz, dolayısıyla buradan $\textbf{N}$ vektörünün eğrilik çemberinin merkezine doğru olduğunu çıkartabiliriz. Yani bulunduğumuz $\alpha(s)$ noktasından normal yönünde $\frac{1}{\kappa(s)}$ miktarında ilerlersek bu çemberin merkezine ulaşırız. İşte biz her $s$ için bu eğrilik çemberlerinin merkez noktalarının kümesine evolute diyeceğiz. Anladınız di' mi neden Türkçeleştiremediğimi? Hadi tanıma geçelim.

Tanım (Evolute)

$\alpha:I\rightarrow \mathbb{R}^3$ yay uzunluğu parametresine sahip bir düzgün eğri olmak üzere $\beta:I\rightarrow \mathbb{R}^3$,

$$\beta(s)=\alpha(s)+\frac{1}{\kappa(s)}\textbf{N}(s)$$

eğrisine $\alpha$ eğrisinin evolute'u denir.

Şimdi belli başlı eğrilerin evolute eğrilerine bakacağız.

Örnek

Aslında evolute kavramı modern diferansiyel geometriden bayağı eski bir kavram. Te Apollonios'un zamanlarında Antik Yunan'da konik eğrilerle uğraşmak modaydı. O zamanın geometri bilgisiyle uğraşılabilecek en karmaşık eğriler onlardı çünkü. Birazdan göreceğiz ki evolute'lar en çok konik eğrilere yakışıyor. Lakin evolute kavramı ilk olarak meşhur sarkaçlar ve 'tautochrone' eğrisinin problemiyle konuşulur oldu. Bu örnekte esas yapmak istediğim şey bu kavramın sarkaçlar ve tautochrone eğrisi bulmayla olan ilişkisi. Bir cycloid eğrisi $x=r(\theta-\sin\theta)$, $y=r(1-\cos\theta)$ parametrizasyonu ile verilen eğridir, burada $r$ sabittir. Basitlik olması açısından $r=1$ alalım. Bu eğrinin eğriliği

$$\kappa(\theta)=\frac{\cos\theta-1}{(2-2\cos\theta)^{3/2}}$$

buradan normal vektörü de rahatlıkla hesaplayabilirsiniz(siz kağıt kalem, ben python ile), ve günün sonunda evolute'unuzun parametrik denklemi $x=\theta+\sin\theta$, $y=\cos\theta-1$ olarak karşımıza çıkar ki bu da kaydırılmış bir cycloid'den başkası değildir, yani:

Teorem

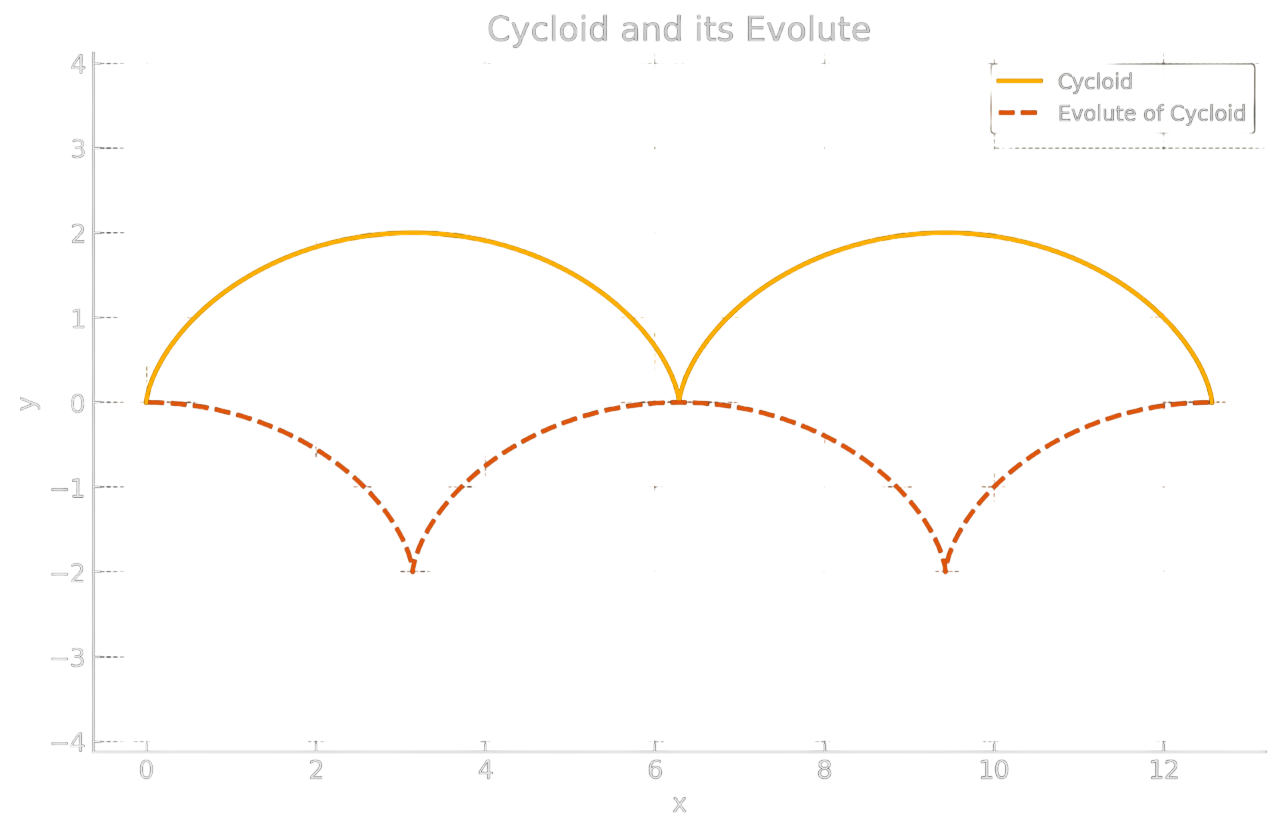
$\alpha$ bir cycloid eğrisi ise evolute'u da bir cycloid eğrisi olacaktır.

Aşağıdaki görselde yukarıda verilen örneğin bir görselleştirmesini bulabilirsiniz.

Örnek

$\alpha$ eğrisi bir çember olmak üzere bu eğrinin evolute'u tek bir nokta belirtir. Bunun sebebini direkt açıklamak yerine bir ipucu vereceğim: evolute'un informal tanımına bakın.

Örnek

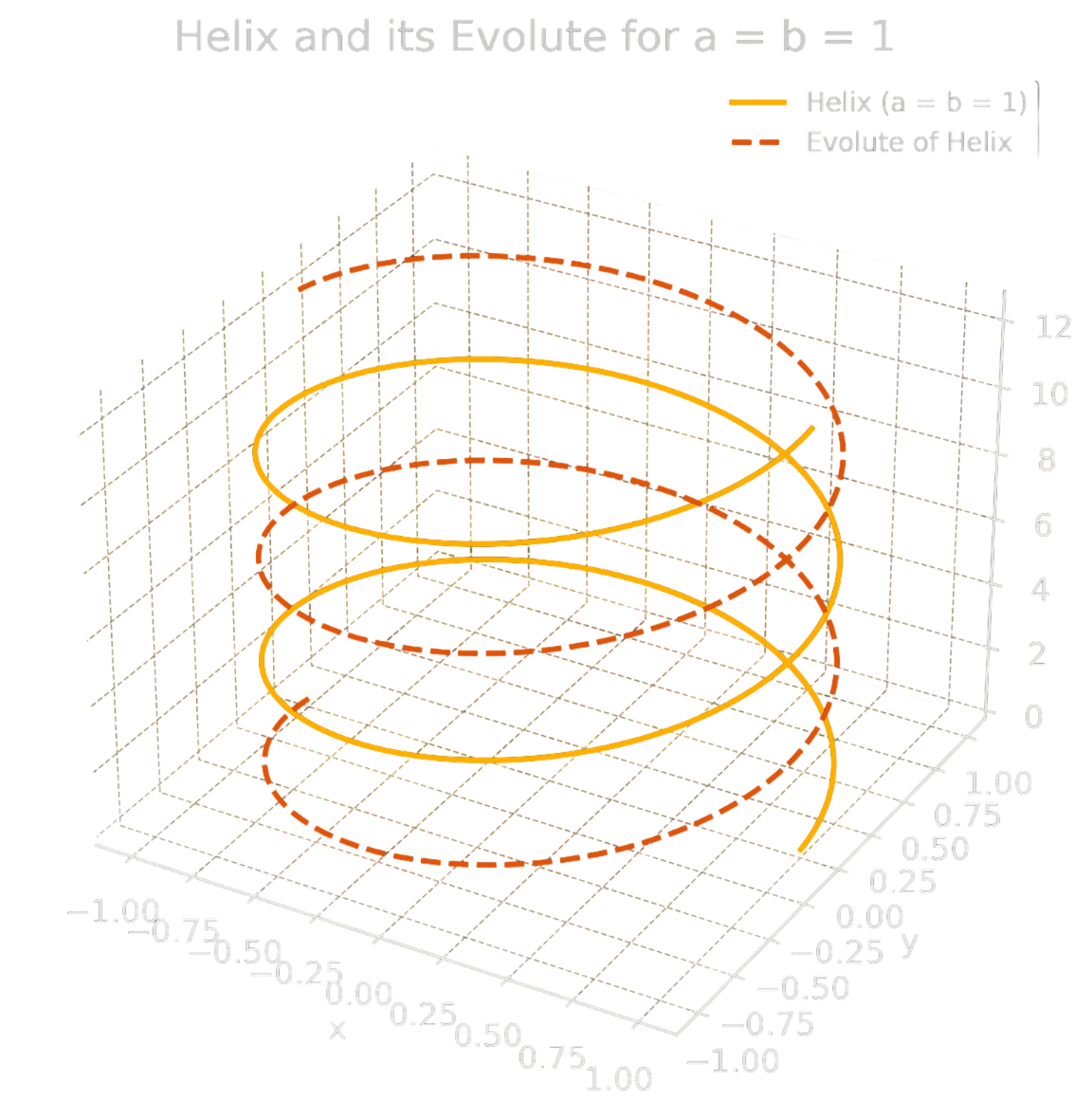
Helis için bakalım, bir helisin evolute'u gene bir helistir fakat oryantasyonu farklıdır. Yani uçları ters yöne bakan iki yay gibi düşünün. Aşağıda $\alpha(s)=(\cos s,\sin s, s)$ helisi ve onun evolute'unun grafiğini bulabilirsiniz.

Bu örnekler daha da uzatılabilir, lakin konunun anlaşıldığını düşünüyorum. Bu bölümde bir eğrinin eğriliği ve burulmasıyla eğriyi tahmin etmece oynayıp ardından bir eğrinin eğriliğinden ve diğer Frenet çatısı elemanlarından başka eğriler türettik. Görüyorsunuz ki eğriler bir derya deniz kulaçla kulaçla bitmez. Bizden de bu bölümlük bu kadar. Bir sonraki bölüm biraz süprisz olacak çünkü ya Öklid uzayında yüzeylere geçeceğim ya da Minkowski uzayında eğrilere bakmaya başlayacağım. Kalın sağlıcakla!